If you know of any better way, please do let me know in the comments.
In my exercise of valuing ($OCO) a copper settlement, someone asked me how to think about the future of the commodity. Here is a logical way to do it: let the market tell you what it thinks.
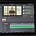
You can go to your broker and select “/HG” (copper futures), then display the options that are traded on them.
Go to the timeframe you have in mind and look for 'delta'. Delta can be used as a proxy for the probabilities of reaching that price from today.
In this case, the odds of copper reaching $4 in 650 days are 51.2%.
Remember, you are thinking about odds, so keep that in mind. Copper is currently at $3.7, and if you look at this chart, it only gives a 62% chance of being at that price. This isn't necessarily because the market expects it to fall, but because as you project into the future, the possibilities of different scenarios also expand.
Using options to determine the odds of a future price in commodities involves understanding the pricing models of options, such as the Black-Scholes model for European options or the Binomial model for American options. These models consider several factors including the current price of the underlying commodity, the strike price of the option, the time until expiration, the risk-free interest rate, and the volatility of the underlying commodity's price.
Here is a basic framework of how you might use options to estimate the probability of a commodity reaching a certain price in the future:
Identify the Option Prices: Start by finding the prices of at-the-money (ATM), in-the-money (ITM), and out-of-the-money (OTM) options for the commodity in question. Both call and put options can provide valuable information.
Implied Volatility: Use the prices of these options to back out the implied volatility of the commodity. Implied volatility is a measure of the market's forecast of a movement in the commodity’s price and is expressed as an annualized percentage. Higher implied volatility means that the market expects a greater chance of the commodity price moving up or down.
Use Pricing Models: Plug the implied volatility into an option pricing model. For simplicity, we’ll use the Black-Scholes model. This model will allow you to calculate the theoretical price of an option given certain variables. It's important to note that the Black-Scholes model assumes constant volatility and interest rates, and it does not consider dividends.
Delta as a Proxy for Probability: The delta of an option can serves as a rough estimate of the probability that the option will expire in-the-money. For instance, an option with a delta of 0.25 theoretically has a 25% chance of expiring in-the-money.
Scenario Analysis: By looking at various strike prices and their corresponding deltas, you can build a probability distribution of future prices. You can do this by looking at a range of strike prices and noting the delta for each.
Adjust for Time: Remember to account for the time until expiration. The more time until an option's expiration, the greater the possibility that the commodity could reach a certain price. Time decay, or theta, will affect the option's value and thus the implied probability.
Risk-Free Rate: Current interest rates will also affect option prices, as they influence the present value of the option's strike price.
Look at Put-Call Parity: To check for consistency and arbitrage opportunities, ensure that the put-call parity holds for the options on the commodity. Discrepancies here can indicate mispricing or opportunities.
Consider the Entire Volatility Smile or Surface: The volatility smile—or in the case of commodities, often a volatility surface due to the changing nature of volatility over different expiration dates—will give you more detailed insight into what the market thinks about the future volatility of different strike prices.
Consider Market Sentiment and Other Indicators: In addition to pure options pricing, consider market sentiment and technical or fundamental analysis to inform your perspective on where the commodity price may be headed.
Once you’ve done this analysis, you can create a probability distribution of where the market believes the commodity price is likely to be at various points in the future. Remember that these probabilities are not certainties and that options markets reflect the views and sentiments of their participants, which can be influenced by factors beyond traditional market fundamentals.
Lastly, it’s important to note that this method provides a risk-neutral probability, which is different from the actual probability as it doesn't account for investors' risk preferences. Actual probabilities would require adjustments to account for risk aversion or preference among market participants.